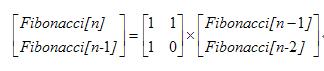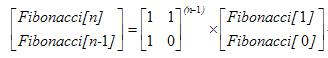本文共 2270 字，大约阅读时间需要 7 分钟。
废话不多说，直接上代码
#include "stdio.h"#include "queue"#include "math.h"using namespace std;/////一：递归实现// 使用公式f[n]=f[n-1]+f[n-2]，依次递归计算，递归结束条件是f[1]=1，f[2]=1。///int fib1(int index) { if(index<1) { return -1; } if(index==1 || index==2) return 1; return fib1(index-1)+fib1(index-2);}/////二：数组实现// 空间复杂度和时间复杂度都是0(n)，效率一般，比递归来得快。///int fib2(int index){ if(index<1) { return -1; } if(index<3) { return 1; } int *a=new int[index]; a[0]=a[1]=1; for(int i=2;i 七：矩阵乘法
最后一种方法不是一种实用的方法，也比较难以想到，其算法实现也比较复杂，在此单述。
我们将数列写成：
Fibonacci[0] = 0，Fibonacci[1] = 1
Fibonacci[n] = Fibonacci[n-1] + Fibonacci[n-2] (n >= 2)
可以将它写成矩阵乘法形式：
将右边连续的展开就得到：
下面就是要用O(log(n))的算法计算：
#includestruct Matrix2By2{ Matrix2By2 ( long long m00 = 0, long long m01 = 0, long long m10 = 0, long long m11 = 0 ) :m_00(m00), m_01(m01), m_10(m10), m_11(m11) { } long long m_00; long long m_01; long long m_10; long long m_11;};Matrix2By2 MatrixMultiply ( const Matrix2By2& matrix1, const Matrix2By2& matrix2 ){ return Matrix2By2( matrix1.m_00 * matrix2.m_00 + matrix1.m_01 * matrix2.m_10, matrix1.m_00 * matrix2.m_01 + matrix1.m_01 * matrix2.m_11, matrix1.m_10 * matrix2.m_00 + matrix1.m_11 * matrix2.m_10, matrix1.m_10 * matrix2.m_01 + matrix1.m_11 * matrix2.m_11);}Matrix2By2 MatrixPower(unsigned int n){ Matrix2By2 matrix; if(n == 1) { matrix = Matrix2By2(1, 1, 1, 0); } else if(n % 2 == 0) { matrix = MatrixPower(n / 2); matrix = MatrixMultiply(matrix, matrix); } else if(n % 2 == 1) { matrix = MatrixPower((n - 1) / 2); matrix = MatrixMultiply(matrix, matrix); matrix = MatrixMultiply(matrix, Matrix2By2(1, 1, 1, 0)); } return matrix;}long long fib7(unsigned int n){ int result[2] = {0, 1}; if(n < 2) return result[n]; Matrix2By2 PowerNMinus2 = MatrixPower(n - 1); return PowerNMinus2.m_00;}//简单的测试int main(){ printf("%d\n",fib7(10)); return 0;}
转载于:https://www.cnblogs.com/hdk1993/p/4366534.html